本記事は2024大学入学共通テスト最前線②　英語　リスニングの続きの内容です。こちらも併せてご覧ください。

【数学IA】
三角比の理解を問う問題正答率が15.4％と低かった測量問題　

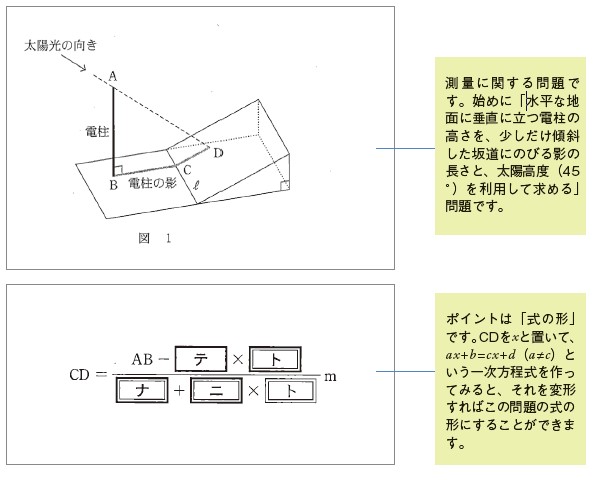
　数学Ｉ・Ａの第１問〔２〕は測量に関する問題です。始めに「水平な地面に垂直に立つ電柱の高さを、少しだけ傾斜した坂道にのびる影の長さ、太陽高度（45°）を利用して求める」問題が出題されました。そこからさらに、わかった電柱の高さを前提として、太陽高度が42°のときの電柱の坂道部分の影の長さCD を表す式を、正しい三角比を当てはめて表します。こちらはかなり難易度が高く、東進生の平均正答率も15. ４％と非常に低い結果となりました。

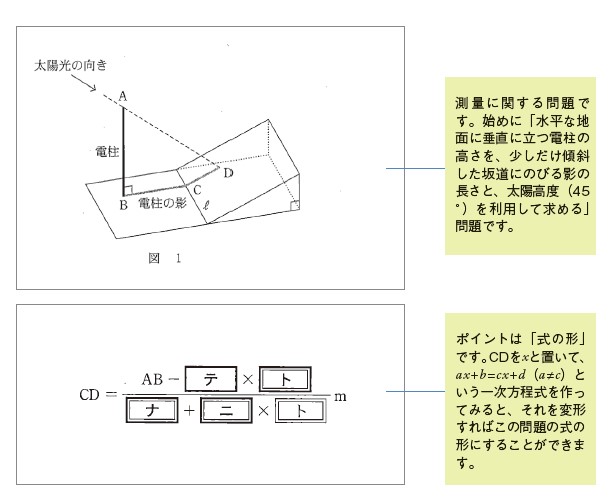
式の形から類推する
　問題の式の空欄がテ、ト、ナ、ニと４つもあるので、どうアプローチするか検討がつかない人も多いかと思います。ポイントは「式の形」です。CDをxと置いて、ax+b=cx+d（a≠c）という一次方程式を作ってみると、それを変形すればこの問題の式の形にすることができます。また共通テストの問題の特徴として、問題文に何も誘導するような記述がなくいきなり答えを出せと求められた場合、その前の設問で行った計算にヒントがあることがほとんどです。前の設問は、∠APBが45°のときのBEとEDの長さを求めよという問題でした。CDをxと置くとBE=xsin θ、ED=7+xcos θになります。この設問ではD E とA E の比がt a n　ですので、左記の式を得ることができます。この式の分母を払えばxの一次方程式が得られますから、解答欄を埋める答えが自動的にわかります。